Một trong các cách tính tích phân bội là chuyển tích phân bội về tích phân lặp. Dưới đây ta nhìn việc chuyển tích phân hai lớp sang tích phân lặp qua ảnh động.
Trường hợp đơn giản nhất: tích phân trên hình vuông có các cạnh song song với các trục
$$\iint\limits_{[0, 2]^2}f(x, y)dxdy.$$

Với mỗi $x\in [0, 2]$ các đoạn đỏ là hằng theo $x$, đều bằng $[0, 2]$. Ta chuyển sang tích phân lặp
$$\iint\limits_{[0, 2]^2}f(x, y)dxdy=\int_0^2 dx \left(\int_0^2 f(x, y)dy\right).$$
Vẽ hình trên trong Maple như sau:
> with(plots); with(plottools)
> F := proc (t) plots[display](plottools[rectangle]([0,0], [t, 2], color= blue, thickness=5), plottools[line]([t, 0], [t, 2], color = red, thickness = 5)) end proc:
> animate(F, [theta], theta = 0 .. 2, background = display(rectangle([0, 0], [2, 2], color = green)), trace = 10, scaling = constrained, axes = none)
Ví dụ đơn giản tiếp theo: tích phân trên hình thoi
$$\iint\limits_{|x| +|y| \le 1} f(x, y)dxdy.$$
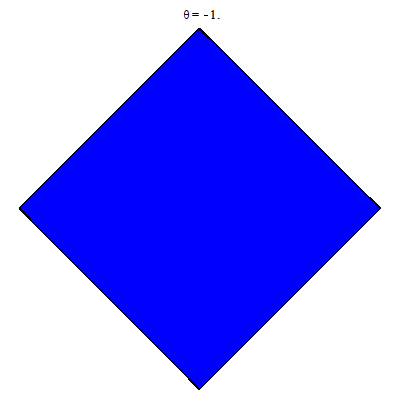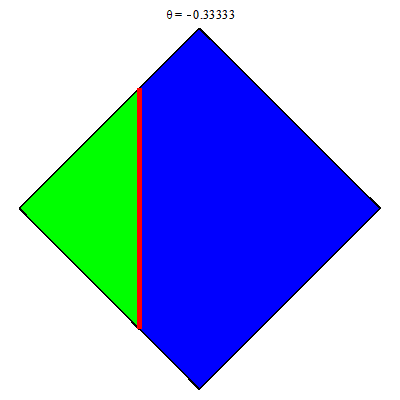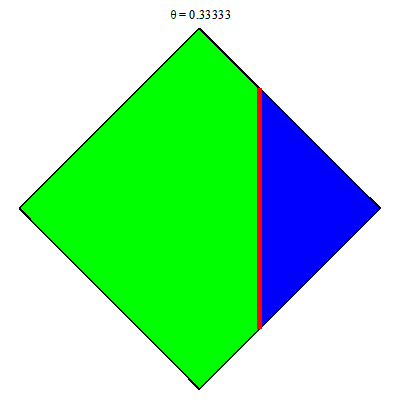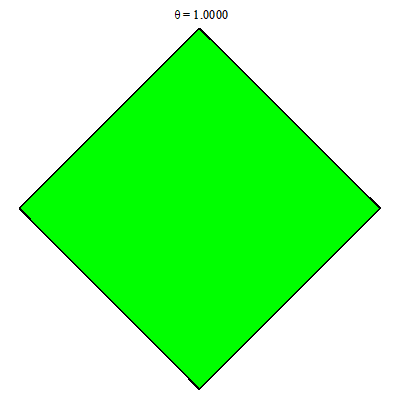
Với mỗi $x\in [-1, 1]$ các đoạn đỏ không còn là hằng theo $x$, cụ thể $[|x|-1, 1-|x|]$. Ta chuyển sang tích phân lặp
$$\iint\limits_{|x|+|y|\le 1}f(x, y)dxdy=\int_{-1}^1 dx \left(\int_{|x|-1}^{1-|x|} f(x, y)dy\right).$$
Vẽ hình trên trong Maple như sau:
> psi := proc (t) options operator, arrow; piecewise(-1 < t and t <= 0, abs(t)-1, 0 < t and t < 2, -1) end proc
> F := proc (t) plots[display](plottools[line]([t, abs(t)-1], [t, 1-abs(t)], color = red, thickness = 5), plottools[polygon]([[-1, 0], [min(t, 0), psi(t)], [t, abs(t)-1], [t, 1-abs(t)], [min(t, 0), -psi(t)]], color = green, thickness = 5)) end proc;
> animate(F, [theta], theta = -1 .. 1, background = display(polygon([[-1, 0], [0, -1], [1, 0], [0, 1]]), color = blue), scaling = constrained, axes = none);
Ví dụ tiếp phức tạp hơn một chút: tích phân trên "đồng tiền vạn lịch"
$$\iint\limits_{x^2+y^2\le 4 \atop \max\{|x|, |y|\}\ge 1} f(x, y) dxdy.$$
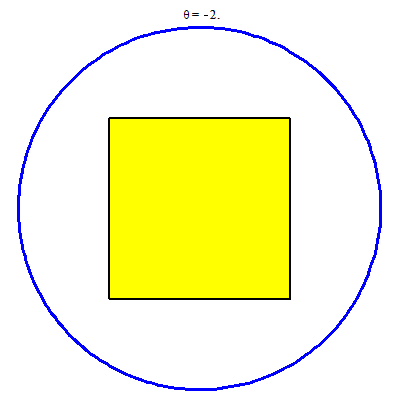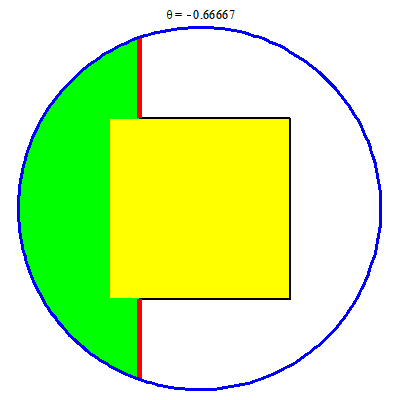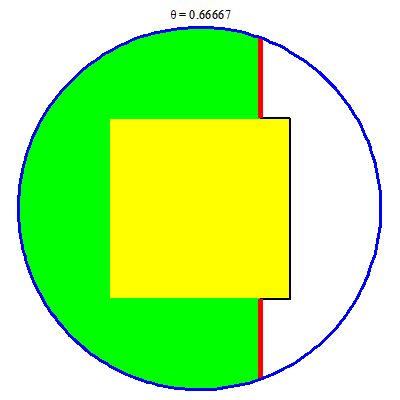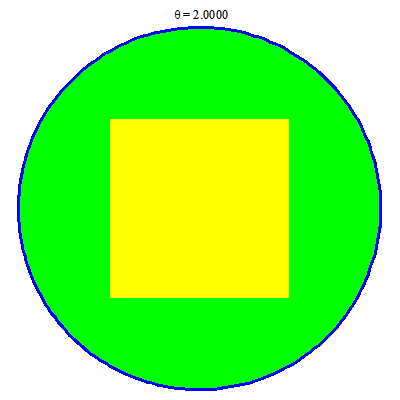
Với mỗi $x\in [-2, 2]$ các đoạn đỏ không những không còn là hằng theo $x$, mà còn có những chỗ nó bị tách đôi (nghĩa là gồm hai đoạn). Cụ thể ta gặp các trường hợp sau:
- Khi $x\in [-2, -1]$ có một đoạn $[-\sqrt{4-x^2}, \sqrt{4-x^2}]$.
- Khi $x\in [-1, 1]$ có hai đoạn $[-\sqrt{4-x^2}, -1]$ và $[1, \sqrt{4-x^2}]$.
- Khi $x\in [1, 2]$ có một đoạn $[-\sqrt{4-x^2}, \sqrt{4-x^2}]$.
Ta chuyển sang tích phân lặp
$$\iint\limits_{x^2+y^2\le 4 \atop \max\{|x|, |y|\}\ge 1} f(x, y) dxdy = $$
$$=\left(\int_{-2}^{-1} + \int_{1}^{2}\right)dx \left(\int_{-\sqrt{4-x^2}}^{\sqrt{4-x^2}} f(x, y)dy\right)+\int_{-1}^1 dx \left(\int_{-\sqrt{4-x^2}}^{-1} + \int_{1}^{\sqrt{4-x^2}}\right) f(x, y)dy.$$
Vẽ hình trên trong Maple như sau:
> f := proc (t) options operator, arrow; piecewise(-2 < t and t < -1, sqrt(4-t^2), -1 < t and t < 1, -1, 1 < t and t < 2, sqrt(4-t^2)) end proc:
> g := proc (t) options operator, arrow; piecewise(-2 < t and t < -1, -sqrt(4-t^2), -1 < t and t < 1, 1, 1 < t and t < 2, -sqrt(4-t^2)) end proc:
> HT := plottools[transform](proc (x, y) [x, y+sqrt(4-x^2)] end proc):
> HD := plottools[transform](proc (x, y) [x, y-sqrt(4-x^2)] end proc):
> F := proc (t) plots[display](HT(plot(g(x)-sqrt(-x^2+4), x = -2 .. t, filled = true, color = green, transparency = 0.)), HD(plot(f(x)+sqrt(-x^2+4), x = -2 .. t, filled = true, color = green, transparency = 0.)), plottools[line]([t, -sqrt(4-t^2)], [t, f(t)], color = red, thickness = 5), plottools[line]([t, sqrt(4-t^2)], [t, g(t)], color = red, thickness = 5)) end proc:
> v1 := polygon([[-1, -1], [1, -1], [1, 1], [-1, 1]], color = yellow):
> c1 := circle([0, 0], 2, color = blue, thickness = 3):
> animate(F, [theta], theta = -2 .. 2, background = display(c1, v1, filled = true), scaling = constrained, axes = none);
Ngoài việc dùng Fubini, việc sử dụng hệ tọa độ cực cũng là cách tốt để tính tích phân hai lớp. Với đồng tiền vạn lịch ở trên ta có hai cách nhìn qua hệ tọa độ cực như sau:
C1:
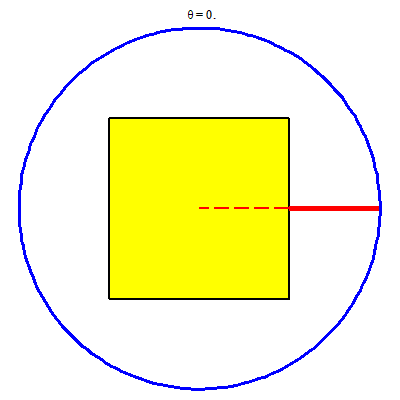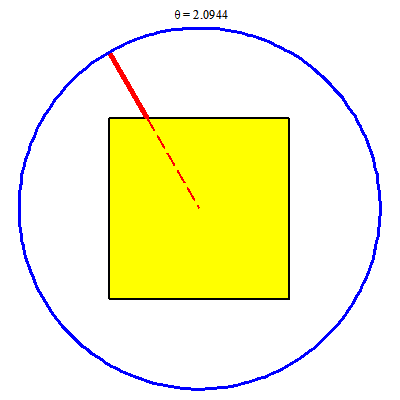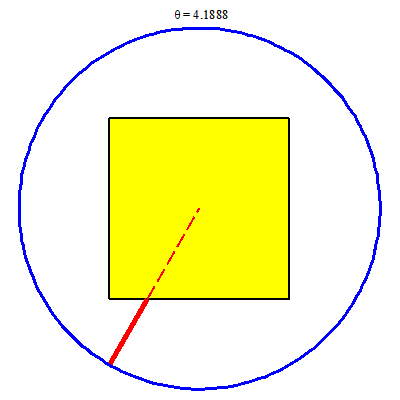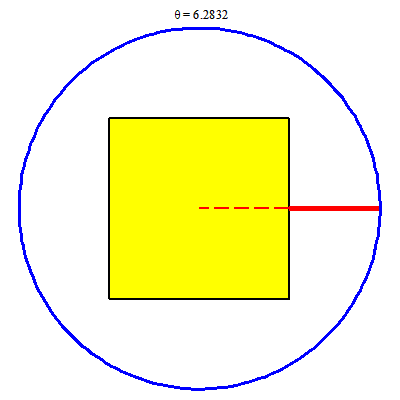
Vẽ trong Maple
> h := proc (t) options operator, arrow; piecewise(0 <= t and t <= (1/4)*Pi, 1/cos(t), (1/4)*Pi <= t and t <= (3/4)*Pi, 1/sin(t), (3/4)*Pi <= t and t <= (5/4)*Pi, -1/cos(t), (5/4)*Pi <= t and t <= (7/4)*Pi, -1/sin(t), (7/4)*Pi <= t and t <= (9/4)*Pi, 1/cos(t)) end proc;
> FR := proc (t) plots[display](plottools[line]([h(t)*cos(t), h(t)*sin(t)], [2*cos(t), 2*sin(t)], color = red, thickness = 5), plottools[line]([h(t)*cos(t), h(t)*sin(t)], [0, 0], color = red, thickness = 2, linestyle = dash)) end proc;
> animate(FR, [theta], theta = 0 .. 2*Pi, background = display(c1, v1), scaling = constrained, axes = none);
C2:
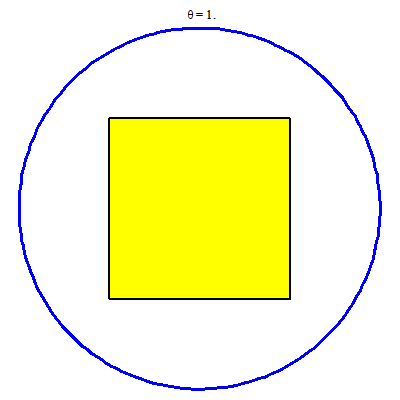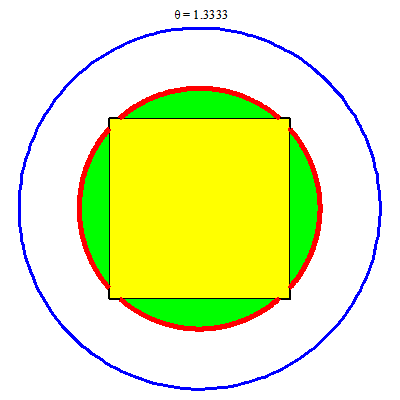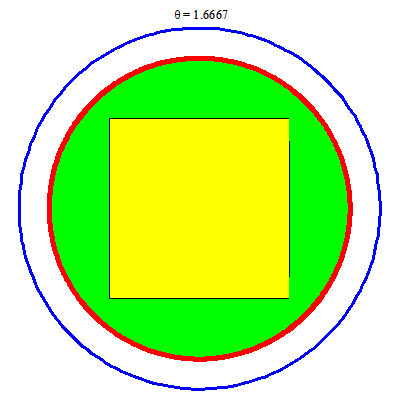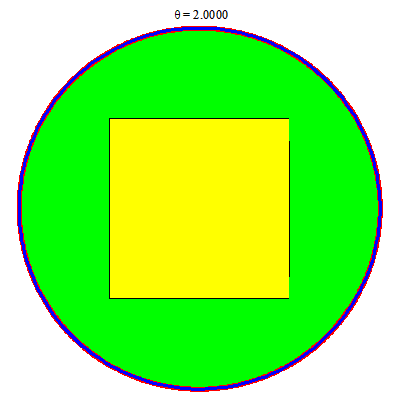
Vẽ trong Maple
> FI := proc (t) plots[display](plot([t*cos(a), t*sin(a), a = -arccos(1/t) .. arccos(1/t)], color = red, thickness = 5), plot([t*cos(a), t*sin(a), a = (1/2)*Pi-arccos(1/t) .. (1/2)*Pi+arccos(1/t)], color = red, thickness = 5), plot([t*cos(a), t*sin(a), a = Pi-arccos(1/t) .. Pi+arccos(1/t)], color = red, thickness = 5), plot([t*cos(a), t*sin(a), a = (3/2)*Pi-arccos(1/t) .. (3/2)*Pi+arccos(1/t)], color = red, thickness = 5)) end proc;
> animate(FI, [theta], theta = 1 .. 2, background = display(c1, v1), scaling = constrained, axes = none);
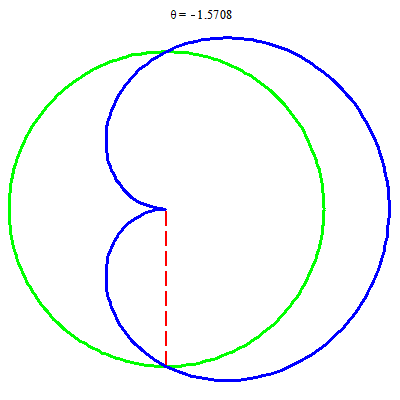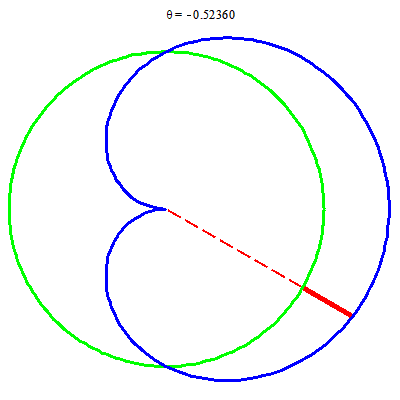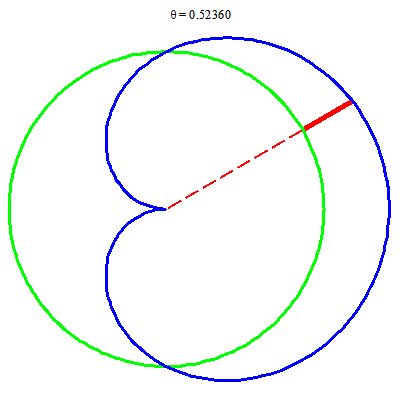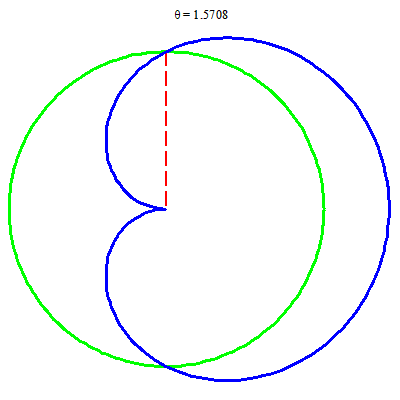
Ví dụ sau cho thấy việc dùng Fubini không dễ, còn hệ tọa độ cực lại không khó: tích phân trên miền trăng khuyết
$$TK=\{(r, \theta):\; -\pi/2\le \theta\le \pi/2, \; 1\le r\le \sqrt{1+\cos\theta}\}.$$
Các hình ảnh trong hệ tọa độ cực của trăng khuyết