Xét bài toán Cauchy cho phương trình Burger sau:
$$\begin{cases}u_t+uu_x &=0 \text{ khi } x\in\mathbb R, t>0, \\ u(x, 0) &=u_0(x) \text{ khi } x\in\mathbb R.\end{cases} $$
Dưới đây ta sẽ giải bài toán Cauchy cho phương trình tổng quát hơn một chút
$$u_t+f(u)u_x=0, x\in\mathbb R, t>0,$$
bằng Maple.
Để cụ thể ta lấy bài 1, đề 3 giữa kỳ lớp CH16-18,
https://bomongiaitich.files.wordpress.com/2017/01/degk_ch16_18_3.pdf
Nhập hàm $f$
> f(u):=1-u^(2):
rồi nhập điều kiện ban đầu
> u0(x):=piecewise(x<0, 0, 0<x<1, 1, x>=1, 2):
Các đường đặc trưng có phương trình
$$x(t)=tf(u_0(\xi))+\xi$$
và được vẽ nhờ Maple
> data := [];
> for n from -10 to 15 do data := [op(data), [t*f(u0((1/5)*n))+(1/5)*n, t, t = 0 .. 1]] end do;
> plot(data);
Ta có hình vẽ:
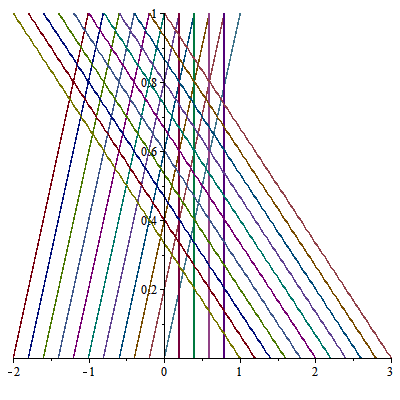
Từ đây ta giải được nghiệm ở miền chỉ có một đường đặc trưng đi qua
$$u(x, t)=\begin{cases} 0 \text{ khi } x<\min\{0, 1-3t\}, t>0, \\ 1 \text{ khi } t<x<1-3t, t>0, \\ 2 \text{ khi } x>\max\{1, t\}, t>0.\end{cases}$$
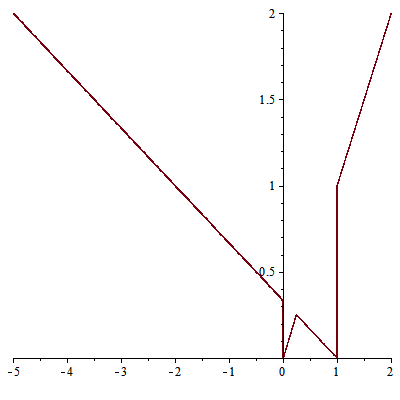
Ta có các điểm bắt đầu xuất hiện sốc $(0, 0), (1, 0).$ Điều kiện Rankine-Hugoniot được tính qua các bước
> F(u):=int(f(x), x=0..u);
> a(u, v):=(F(u)-F(v))/(u-v);
Sốc bắt đầu tại $(0, 0)$ do giao giữa vùng $u=0$ bên trái và $u=1$ bên phải nên ta có đường sốc từ điểm này
> s0(t):=a(0, 1)*(t-0)+0;
Sốc bắt đầu tại $(1, 0)$ do giao giữa vùng $u=1$ bên trái và $u=2$ bên phải nên ta có đường sốc từ điểm này
> s1(t):=a(1, 2)*(t-0)+1;
Hai đường sốc này giao nhau tại thời điểm
> Student:-Calculus1:-Roots(s0(t)-s1(t), numeric);
[0.5000000000]
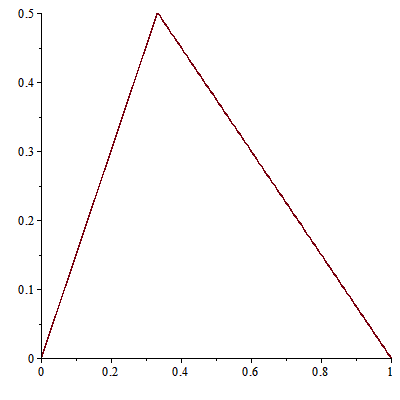
Ta giải được nghiệm trước thời điểm có giao $t=1/2$
> u(x, t):=piecewise(x<s0(t), 0, s0(t)<x<s1(t), 1, x>s1(t), 2):
> plot3d(u(x, t), x = -2 .. 2, t = 0 .. 1/2);
> animate(plot, [u(x, t), x = -2 .. 2], t = 0 .. 1/2)
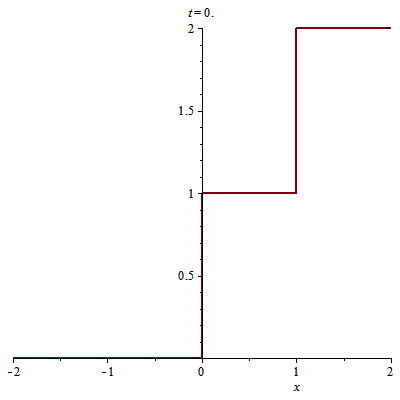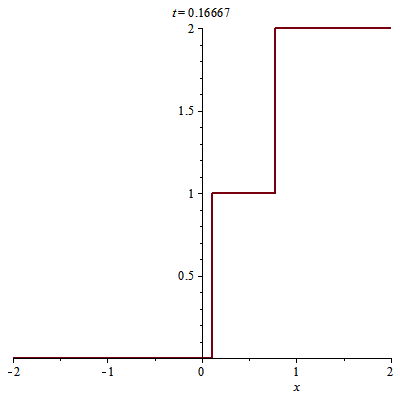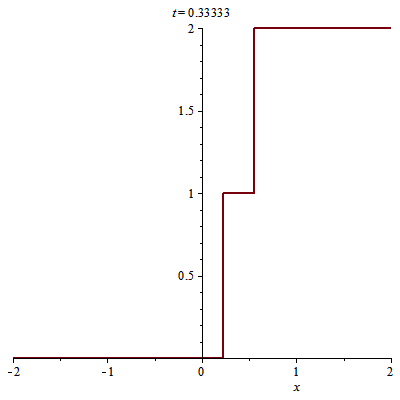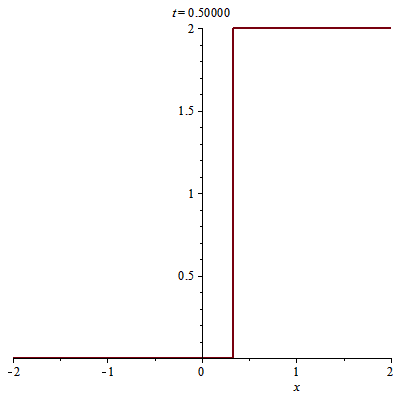

Sau $t=1/2$ các đường đặc trưng xuất phát $(x, 0), x<0,$ và xuất phát $(x, 0), x>1$ lại gây ra sốc, còn các đường đặc trưng xuất phát $(x, 0), 0<x<1,$ bị chặn lại bởi các đường sốc $s0(t), s1(t)$. Sốc này xuất phát tại điểm $(s0(1/2), 1/2)$ giữa miền $u=0$ bên trái và $u=2$ bên phải nên có đường sốc
> s2(t):=a(0, 2)*(t-1/(2))+s0(1/2);
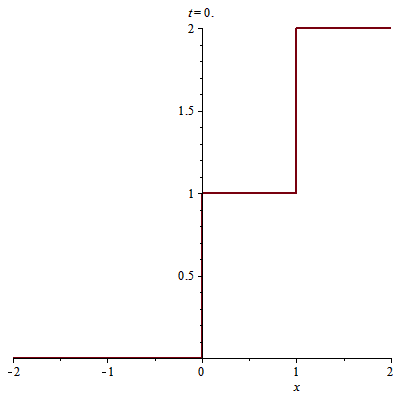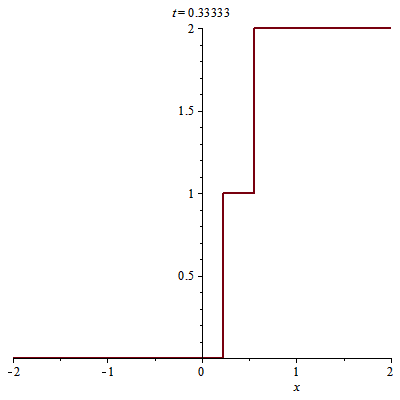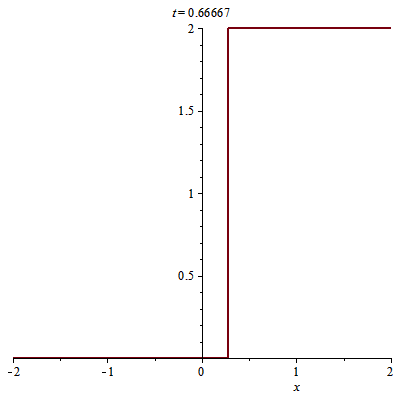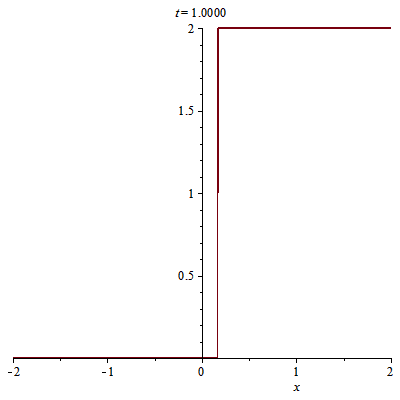
Ta có nghiệm sau $t=1/2$:
> u(x, t):=piecewise(x<s2(t), 0, x>s2(t), 2);
Hình ảnh của nghiệm

Quay trở lại phương trình Burger ở đầu bài, các bạn thử xem các bước ở trên thay đổi như nào với điều kiện ban đầu cụ thể
$$u_0(x)=\begin{cases}2 \text{ khi } x<0,\\ 1 \text{ khi } 0<x<1, \\ 0 \text{ khi } x>1.\end{cases}$$


