Trong bài trước
http://mim.hus.vnu.edu.vn/vi/content/t%E1%BA%A1o-%E1%BA%A3nh-%C4%91%E1%B...
tôi đã trình bày cách giải bài toán biên hỗn hợp cho phương trình truyền sóng nhờ chuỗi Fourier (phương pháp tách biến). Dưới đây tôi sẽ trình bày cách giải bằng sóng tiến - sóng lùi. Để cụ thể ta sẽ giải bài 1 trong đề thi cuối kỳ cho lớp K59TN
https://bomongiaitich.files.wordpress.com/2017/01/cuoikyk59tn.pdf
Ta bắt đầu bằng việc nhập các dữ liệu
> c := 1: # toc do lan truyen
> L := Pi: # chieu dai soi day
> f := proc (x) options operator, arrow; 0 end proc: # trang thai ban dau
> g := proc (x) options operator, arrow; piecewise(0 <= x and x < (1/2)*L, 0, (1/2)*L <= x and x <= L, 1) end proc: # van toc ban dau
Hình ảnh điều kiện ban đầu

Do điều kiện biên đã cho là điều kiện hai đầu tự do nên ta thác triển chẵn, tuần hoàn chu kỳ $2L$ các điều kiện ban đầu:
> f1 := proc (x) options operator, arrow; piecewise(0 < x and x < L, f(x), L < x and x < 2*L, f(2*L-x)) end proc: f2(x):=f1(x-2*L*floor(x/(2*L))):
> g1 := proc (x) options operator, arrow; piecewise(0 < x and x < L, g(x), L < x and x < 2*L, g(2*L-x)) end proc: g2(x):=g1(x-2*L*floor(x/(2*L))):
Hình ảnh sau thác triển của điều kiện ban đầu

Tiếp đến tính nguyên hàm của vận tốc ban đầu:
> proc (x) options operator, arrow; (int(g1(y), y = 0 .. x))/c end proc: h1(x):=h(x-floor(x/(2 L))*2 L)+floor(x/(2 L))*h(2 L):
Hình ảnh nguyên hàm

Tạo sóng tiến, sóng lùi
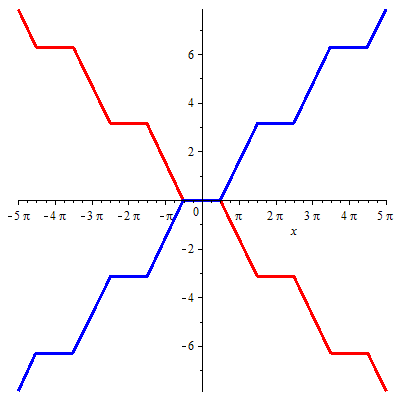
> F(x):=f2(x)-h1(x); G(x):=f2(x)+h1(x); plot([F(x), G(x)], x=-5*L..5*L, color=[red, blue], thickness=3)
Hình ảnh sóng tiến, sóng lùi:
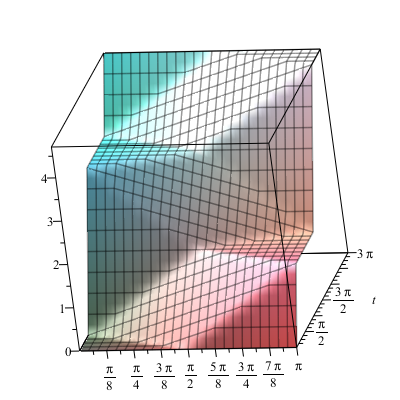
Hình ảnh của nghiệm
> animate(plot, [[F(-c*t+x), G(c*t+x), (F(-c*t+x)+G(c*t+x))*(1/2)], x = 0 .. L], t = 0 .. 3*L, color = [red, blue, green], thickness = 3);
> plot3d((F(-c*t+x)+G(c*t+x))*(1/2), x = 0 .. L, t = 0 .. 3*L);